Cách tính diện tích toàn phần và công thức của hình nón

Các bạn muốn ôn lại kiến thức về hình nón, công thức và cách tính diện tích toàn phần của hình nón để áp dụng trong học tập, trong công việc hay trong cuộc sống. Vậy mời các bạn cùng tham khảo bài viết dưới đây để biết công thức & cách tính diện tích toàn phần hình nón.

Dưới đây Pgdphurieng.edu.vn.vn chia sẻ đến các bạn khái niệm hình nón, công thức và cách tính diện tích toàn phần hình nón, mời các bạn cùng theo dõi.

Hình nón là gì?

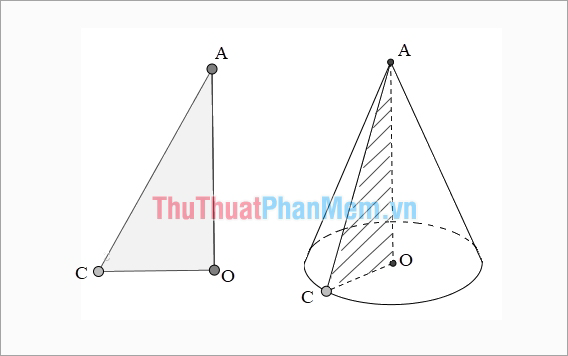
Khi ta quay tam giác vuông OAC một vòng quanh cạnh góc vuông OA cố định thì ta được hình nón. Như vậy hình nón được tạo bởi:

• Cạnh OC tạo nên đáy hình nón là một đường tròn tâm O.
• Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh.
• A là đỉnh của hình nón và AO là đường cao của hình nón.

Công thức tính diện tích toàn phần hình nón

Giả sử các bạn có hình nón như sau:

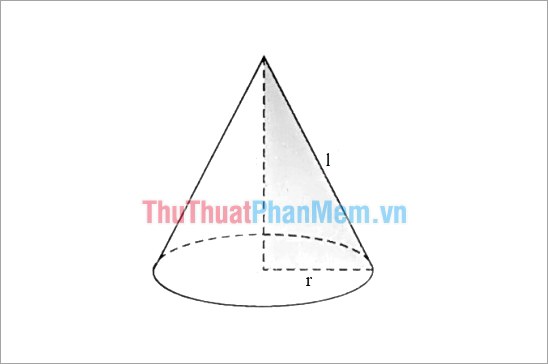
Diện tích toàn phần của hình nón bằng diện tích xung quanh của hình nón cộng với diện tích đáy. Công thức tính diện tích toàn phần:

({S_{tp}} = {S_{xq}} + {S_đ} = pi rl + pi {r^2})

Trong đó:

• ({S_{tp}}) là diện tích toàn phần của hình nón.
• ({S_{xq}}) là diện tích xung quanh của hình nón.
• ({S_{đ}}) là diện tích đáy của hình nón.
• π là hằng số (=3.14159265359)
• r là bán kính mặt đáy của hình nón.
• l là độ dài đường sinh của hình nón.

Cách tính diện tích toàn phần hình nón

Để tính diện tích toàn phần của hình nón các bạn cần biết diện tích xung quanh và diện tích đáy của hình nón, hoặc nếu chưa biết thì các bạn cần biết bán kính r và độ dài đường sinh l.

1. Nếu biết diện tích xung quanh và diện tích đáy hình nón hay nếu đã biết bán kính r và độ dài đường sinh l thì các bạn chỉ cần áp dụng công thức ({S_{tp}} = {S_{xq}} + {S_đ} = pi rl + pi {r^2})
2. Nếu chưa biết bán kính r và đường sinh l của hình nón thì các bạn cần tính r và l dựa vào những gì đề bài cho.
3. Sau khi đã tính bán kính r và đường sinh l thì các bạn sử dụng công thức tính diện tích toàn phần hình nón ở trên để tính.

Ví dụ: Cho hình nón có độ dài đường sinh là 10 cm, độ dài đường cao là 6 cm. Tính diện tích toàn phần của hình nón.

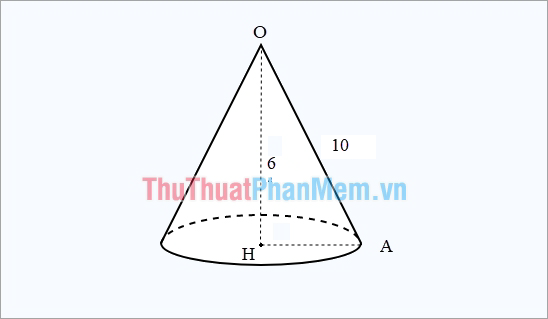
Giả sử hình nón có đỉnh là O, tâm đáy là H, A là một điểm thuộc đường tròn đáy. Như vậy ta sẽ có: OA = 10 cm, OH = 6 cm.

Trong tam giác vuông OHA, (r = HA = sqrt {O{A^2} – O{H^2}} = sqrt {{{10}^2} – {6^2}} = 8cm)

Áp dụng công thức tính diện tích toàn phần hình nón ta có:

({S_{tp}} = pi rl + pi {r^2} = pi .8.10 + pi {.8^2} = 80pi + 64pi = 144pi )

Như vậy diện tích toàn phần hình nón là (144pi c{m^2}).

Như vậy trên đây bài viết đã chia sẻ đến các bạn công thức và cách tính diện tích toàn phần của hình nón, hi vọng các bạn sẽ ghi nhớ công thức và áp dụng cách tính diện tích toàn phần hình nón để áp dụng vào các bài tập hay trong cuộc sống.