Cách tính diện tích tam giác bằng công thức Heron – Công thức Heron

Các bạn đang tìm kiếm công thức Heron để tính diện tích tam giác khi biết độ dài 3 cạnh của tam giác. Vậy các bạn hãy cùng tham khảo bài viết dưới đây để biết cách tính diện tích tam giác bằng công thức Heron.

Dưới đây là công thức Heron, cách tính diện tích tam giác bằng công thức Heron, mời các bạn cùng theo dõi.

Công thức Heron là công thức tính diện tích của một tam giác theo độ dài 3 cạnh. Đây là công thức mang tên nhà toán học Heron của Alexandria.

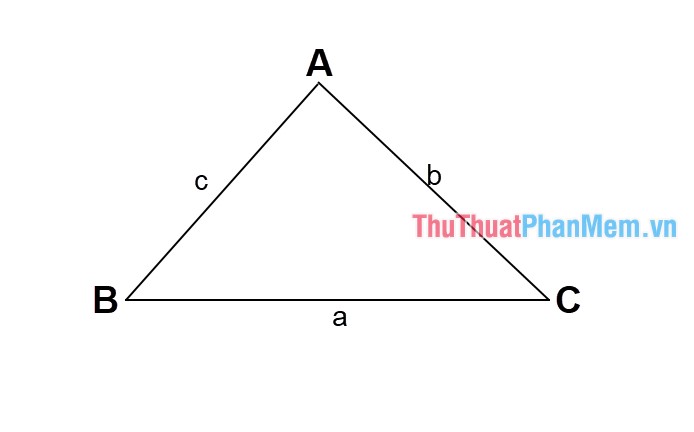
Công thức Heron được viết như sau:

Gọi S là diện tích và độ dài 3 cạnh tam giác lần lượt là a, b và c

[S = sqrt {pleft( {p – a} right)left( {p – b} right)left( {p – c} right)} ]

Với p là nửa chu vi của tam giác.

[p = frac{{a + b + c}}{2}]

Công thức Heron còn có thể được viết lại bằng:

[S = frac{{sqrt {left( {a + b + c} right)left( {a + b – c} right)left( {b + c – a} right)left( {c + a – b} right)} }}{4}]

[S = frac{{sqrt {2left( {{a^2}{b^2} + {a^2}{c^2} + {b^2}{c^2}} right) – left( {{a^4} + {b^4} + {c^4}} right)} }}{4}]

[S = frac{{sqrt {{{left( {{a^2} + {b^2} + {c^2}} right)}^2} – 2left( {{a^4} + {b^4} + {c^4}} right)} }}{4}]

Cách chứng minh công thức Heron

Cách chứng minh này sử dụng đại số và lượng giác

Gọi a, b, c lần lượt là 3 cạnh của tam giác và A, B, C lần lượt là các góc đối diện của các cạnh. Theo hệ quả định lý cosin, ta có:

[cos left( C right) = frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}]

Từ đó:

[sin left( C right) = sqrt {1 – {{cos }^2}left( C right)} = frac{{sqrt {4{a^2}{b^2} – {{left( {{a^2} + {b^2} – {c^2}} right)}^2}} }}{{2ab}}]

Dựa vào đường cao và sin của góc C. Ta có công thức tính diện tích tam giác ABC:

Vậy nếu các bạn muốn tính diện tích tam giác với ba cạnh a, b, c thì các bạn cần tính nửa chu vi của tam giác với công thức:

[p = frac{{a + b + c}}{2}]

Sau đó áp dụng công thức tính diện tích Heron để tính diện tích tam giác:

[S = sqrt {pleft( {p – a} right)left( {p – b} right)left( {p – c} right)} ]

Trên đây là công thức Heron, cách tính diện tích tam giác bằng công thức Heron. Hi vọng qua bài viết này các bạn sẽ có thêm kiến thức về công thức Heron và áp dụng công thức Heron để tính diện tích tam giác nhanh chóng. Chúc các bạn thành công!